
Signals with shape: why topology matters for modern data?
November 2025
Research
Read more
Based on the article: Topological Signal Processing and Learning: Recent Advances and Future Challenges (Signal Processing, 2025, Vol. 233, 109930) by E. Isufi, G. Leus, B. Beferull-Lozano, S. Barbarossa and P. Di Lorenzo.
Horizon in decision making
When we think about signals—like the sounds we hear, the images we see, or the information we broadcast—we often picture them as values that change over time or space.
However, signals are present in many other domains—flowing through our cities as traffic patterns, across our brains as neural activity, and within our devices as interconnected data streams. In the latter case, the underlying complex system and the structure behind the data—be it the brain, the city or the communication network—shapes how signal behaves and makes conventional signal processing and machine learning techniques obsolete when data lives on such complex, interconnected systems.
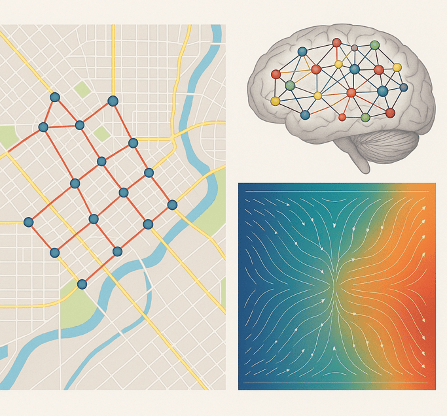
For decades, graphs have been the workhorse for representing the structure of such data, modelling pairwise relationships—e.g., nodes as crossroads, edges as streets, and data as the number of cars recorded at each intersection.
But as real-world systems become more complex—think multi-agent interactions, biological networks, or high-dimensional sensor data—graphs begin to fall short. They can represent pairwise links, but not higher-order relationships: multiway groups and other intricate connections that shape how information truly flows. The question posed in this article is:
How do we process data with such higher-order relationships?
That's exactly what the emerging field of Topological Signal Processing and Learning (TPSL) explores, that is, how mathematics from algebraic topology can extend the foundations of modern signal processing and machine learning beyond graphs—into the realm of geometry and topology.
From Graphs to Topologies: Seeing the Bigger Shape
At the heart of this emerging field is the idea that data often live not just on points or lines, but on topological spaces or shapes. By representing data using mathematical structures called simplicial or cell complexes—generalizations of graphs that can capture triangles, tetrahedra, and higher-dimensional interactions—it is possible to analyze and process signals at multiple levels of connectivity and understand the shape of how information flows.
Tools from algebraic topology— like the Hodge Laplacian make it possible to generalize familiar signal-processing operations—such as filtering, denoising, or spectral analysis—to these richer spaces.
In simple terms: we can now uncover and reveal global structures and hidden patterns like
These tools allow signals defined on nodes, edges, and higher-dimensional entities to be processed jointly, revealing global structures like loops, holes, or surfaces that ordinary graph models simply can't see.
Fourier, but for Topologies
When we think of processing signals, the name of Joseph Fourier, the man who taught us how to decompose signals into fundamental frequencies—Fourier Transform, comes naturally. Topological Signal Processing extends that same intuition. By building on the principles of the Fourier transform for time and space, it is possible to generalize the same idea to data defined over graphs or over general arbitrary topologies. This generalization allows connecting methods and insights across different domains and exploring new avenues in a tractable way.
The topological Fourier Transform allows us to "hear" the fundamental oscillating frequencies of signals over complex structures (arbitrary topologies)—from road networks to neural circuits. For instance, in systems with edge flows (like traffic or electrical currents), this approach helps identify circulating versus diverging components—concepts familiar from physics but now applied to abstract data domains.
While generally abstract, this view not only provides techniques to unravel new insights from data, but also to develop convolutional filtering, sampling, and interpolation techniques, as well as build principled Topological Machine and Deep Learning methods. In the particular case of edge flows, for instance, the topological Fourier transform has intuitive ties with vector calculus and identifies the solenoidal and irrotational components of signals.
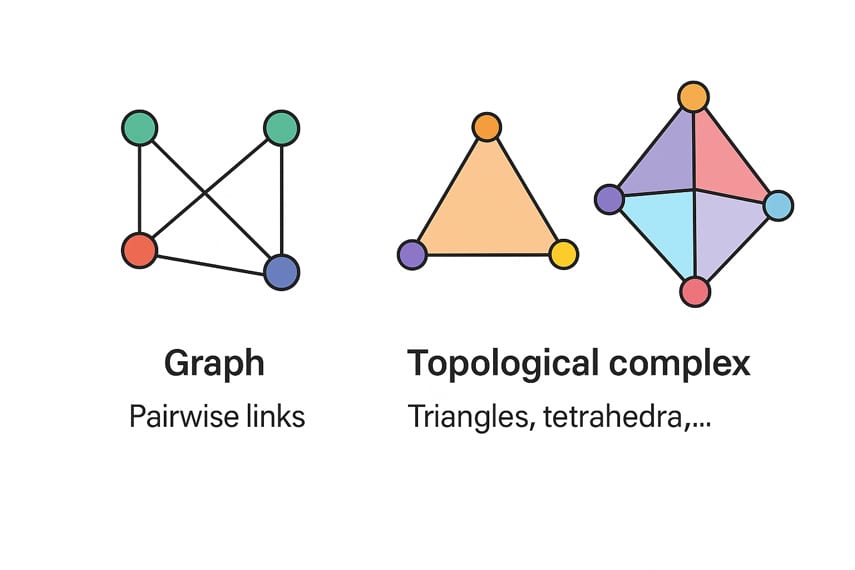
Connecting the Threads
Building on these insights, this paper offers a comprehensive and accessible overview of the field of Topological Signal Processing and Learning (TSPL)—a fast-evolving intersection of Mathematics, Signal Processing, and Machine Learning. It connects threads from diverse areas:
- Graph Signal Processing, which focuses on data over networks;
- Topological Data Analysis, which studies shapes and connectivity in data;
- Topological Machine Learning, which brings these insights into Deep Learning architectures (e.g. Topological Neural Networks)
By weaving these threads together, the authors present a unified framework that clarifies how ideas like the topological Fourier transform, Hodge decomposition, and learning of topologies from data fit into one coherent picture.
New Opportunities and Open Challenges
TSPL methods are already opening doors to new applications—ranging from sensor networks and biological systems to spatiotemporal modeling and Geometric Deep Learning. Yet, the paper highlights key challenges that remain:
- Building computationally efficient algorithms grounded in topological theory;
- Developing data-driven models that can infer topology directly from observations;
- Integrating topological priors seamlessly into modern machine learning frameworks.
At SURE-AI, we will focus on these challenges, not only to transform theoretical insights into powerful algorithms and practical applications, but also develop the AI solutions that remain principled, foundational and tractable, properties much needed to grow trust in these methods and for deployment in critical real-world infrastructure.
It’s an exciting step toward understanding signals not just as data in time or space—but as data with shape.
Keep reading
Double-click to select video


SURE-AI kicks off: “of vital importance to our future”
December 2025
News
Read more
Double-click to select video


Unifying Risk and Belief: A Foundation for Coherent AI Decision-Making
October 2025
Research
Read more
Double-click to select video
En annen sak med en tittel som dette
September 2025
News
Read more
The economics of overlapping generations: a stochastic lens
October 2025
Research
Read more
Double-click to select video


Unifying Risk and Belief: A Foundation for Coherent AI Decision-Making
October 2025
Research
Read more


Beyond the Monolith: How Brain-Inspired AI is Building a More Reliable and Sustainable Future
November 2025
Research
Read more


Signals with shape: why topology matters for modern data?
November 2025
Research
Read more


Why horizon matters more than you think in decision making
November 2025
Research
Read more
Double-click to select video


The economics of overlapping generations: a stochastic lens
October 2025
Research
Read more