News article: New Math Framework Unlocks Safer, More Robust AI Decisions

Golden sunset behind dark mountain silhouettes, with bright sun and clouds.

Unifying Risk and Belief: A Foundation for Coherent AI Decision-Making

October 2025

Research

Read the full preprint here:

Inference as Risk Identification

When a statistician or an AI system tries to learn from data—a process called inference—they are essentially making an educated guess about an uncertain world. The gold standard for this has long been the Bayesian method, which finds the most likely distribution of possibilities (the "posterior") that balances new data with prior knowledge or beliefs.

But what if we could make this guessing game not just more accurate, but fundamentally safer and more flexible to include a broader array of risk preferences?

A new preprint titled "Inference as Risk Identification" proposes a radical mathematical reframing that does exactly that. The work, by Aurya S. Javeed (Sandia National Laboratories), Drew P. Kouri (Sandia National Laboratories), and Thomas M. Surowiec (SURE-AI & Simula Research Laboratory), shows that the result of statistical inference—the model’s distribution of possibilities—can be viewed as a Risk Identifier.

From Best Guess to Safety Buffer

In finance, a risk identifier isn't just an average return; it's a measure that clearly outlines the potential worst-case scenario or the amount of capital needed as a safety buffer.

By showing that the statistical posterior is mathematically equivalent to this kind of tool (specifically, a subgradient of a risk measure), the authors have built a bridge between the world of advanced statistics and the proven framework of computational risk management.

Plot of KL, CS, RY, TV functions vs x. All start at 1, dip near x=1 to 0, then rise.

Line plot comparing four functions (exp, quad, iso, abs) against x-axis.

Four common disutility functions (plotted with a horizontal and a vertical flip to appear as utility functions), as well as their associated divergences: (a) the exponential disutility (exp.) and Kullback-Leibler divergence (KL), (b) a truncated quadratic disutility (quad.) and chi-squared divergence (CS), (c) the isoelastic disutility and Rényi divergence (RY), (d) an absolute disutility and total variation divergence (TV).

This single, powerful insight has three major consequences for how we build and trust our models:

1. Model Stability and Trust:

By defining inference in terms of risk, the authors establish rigorous mathematical guarantees for when a model’s solution exists and how it behaves when fed more and more data. This is crucial for building trust in complex machine learning systems.

2. Robustness Against Bad Data:

The new framework allows researchers to explicitly constrain how far the final result can stray from the initial, trusted knowledge (the "prior"). This leads to a new method called "coherent inference," which creates models that are far more robust and less likely to be derailed by a few pieces of misleading or noisy data.

3. A Computational Breakthrough:

The paper derives simplified, semi-analytic expressions for these risk-based posteriors. This means that solving complex, multi-dimensional inference problems—which are often computational nightmares—can be reduced to solving much simpler, low-dimensional optimization problems. This makes advanced inference techniques dramatically more practical and faster to implement.

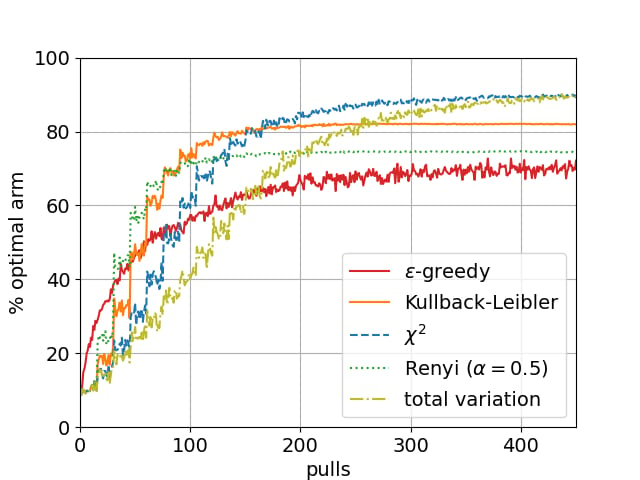
Line graph: % optimal arm vs. pulls for five bandit algorithms (epsilon-greedy, KL, chi-squared, Renyi, total variation).

Coherent Inference can be used to solve problems related to AI and reinforcement learning such as classical multi-armed bandits. Here is an example in solving the 10-armed bandit problem with phi-divergence-constrained posterior updates. The following divergences are considered: Kullback-Leibler, chi-squared, Rényi (alpha=0.5), and total variation. For comparison, the well-known epsilon-greedy heuristic from reinforcement learning is included. For this heuristic, epsilon = 0.2, which is also used as the epsilon in the divergence-constrained settings.

Ultimately, by viewing the act of learning as an act of risk identification, this research provides a powerful, unified mathematical lens. It not only connects classical statistics with modern optimization and utility theory (the economics of decision-making) but also paves the way for a new generation of more reliable, safer, and mathematically grounded AI and data analysis tools.

Check out the full paper for details:

Inference as Risk Identification

This popular science blog article was generated by Gemini, a large language model trained by Google along with modifications by one of the authors.